B - Trees

Let’s talk about B-Trees, LSM Trees are gaining acceptance in the NoSQL realm, but they are not the most common type of index which is used widely. The most famous indexing structure which is used in most of the relational database and a fraction of the non-relational world is B-Tree.

Like Sorted-Segment Tables, B-Trees also keep key-value pairs sorted by key, which allows efficient key-value lookups and range queries. You might even ask why can we use a Hash-Table instead which gives us value lookups on a key in O(n) time. But Hash-Tables are not suitable for doing range-based queries efficiently.

While the log-structured indexes break the database into variable-size segments, typically several megabytes or more in size, and always write a segment sequentially, B-Trees on the other hand break the database down into fixed-size blocks or pages, traditionally 4KB in size(might be bigger as well, sometimes), and read or write one page at a time. This design corresponds more closely to the underlying hardware, as disks are also arranged in fixed-size blocks.

Each page can be identified using an address or location, which allows one page to refer to another: similar to a pointer, but on disk instead of in memory. We can use these page references to construct a tree of pages, as shown below

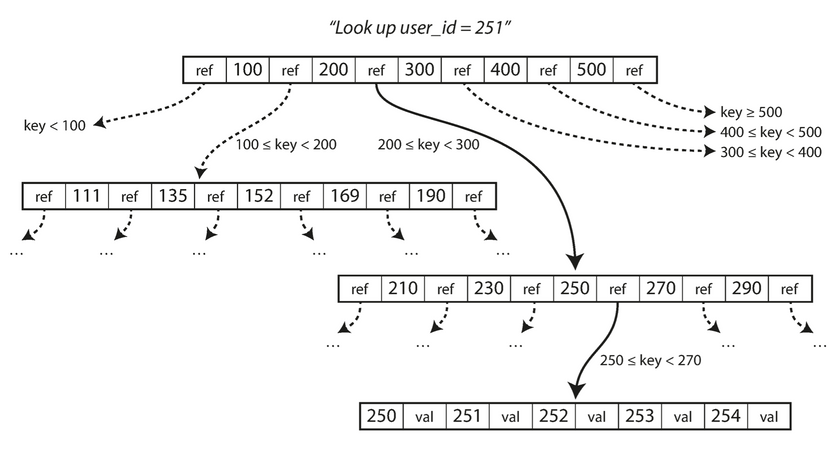
One Page is designated as the root of the tree, whenever a key look up is required on the index, we start here. The page contains several keys and references to child pages. Each child is responsible for a continuous range of keys, and the keys between the references indicate where the boundaries between those range lies.

In the above example, we are searching for key 251, so we know that we need to follow the page reference between boundaries 200 and 300. That takes us to a similar-looking page that further breaks down the 200-300 range into sub-ranges. Eventually we get down to a page containing individual keys(a leaf page), which either contains the value for each key inline or contains references to pages where the values can be found.

The number of references to child pages in one page of the B-tree is called the branching-factor. For example in the above scenario depicted in the image, the branching-factor is 6. In practice, the branching factor depends on the amount of space required to store the page-references and the range boundaries, but typically its in magnitude of several hundred.

If we have to update the value for an existing key in a b-tree, we search for the leaf page containing that key, change the value in that page, write the page back to disk(any references to that page remain valid). If we want to add a new key, we need to find the page whose range encompasses the new key and add it to that page. If there isn’t enough free space in that page to accommodate the new key, it is split into two half full pages, and the parent page is updated to account for the new subdivision key ranges as shown below

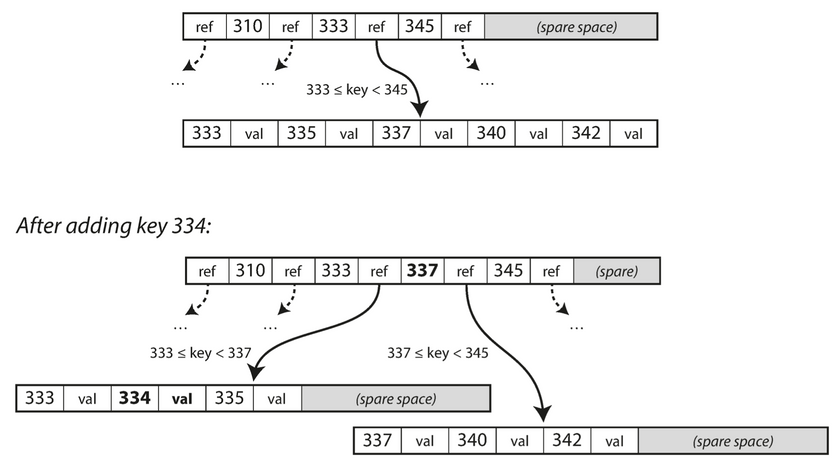
This way we can be assured that the B-Tree is always balanced(if balancing fails the search complexity goes to O(n), refer to self balancing trees like AVL tree for more info on this), so a B-tree with n keys always has a depth of O(log(n)). Most databases can fit into a B-Tree that is three or four-levels deep(depends on the branching factor), so we need not follow many page references to find the page we are searching for. Example: A four-level tree of 4KB pages with a branching factor of 500 can store up to 256TB.

Ensuring reliability in B-Trees

The basic underlying write operation of a B-Tree is to overwrite a page on disk with new data. It is always assumed the write does not change the location of the page, i.e all references to that page remain intact when the page is overwritten. This is in stark contrast to log-structured indexes such as LSM-Trees, which only appends to files(and eventually deletes obsolete files) but never modifies them in place.

We can think of overwriting a page on disk as an actual hardware operation. On the magnetic hard drive, this means moving the disk head to the right place, waiting for the right position on the spinning platter to come around, and then overwriting the appropriate sector with new data. On SSDs, what happens is somewhat more complicated, due to the fact that an SSD must erase and rewrite fairly large block of a storage chip at a time.

Moreover, some operations require several different pages to be overwritten. For example, if we split a page because an insertion caused it to overflow, we need to write two pages that were split, and also overwrite their parent page to update the references to the two child pages. This is a dangerous operation, because if the database crashes after only some of the pages have been written, we end up with a corrupted index(e.g, there may be an orphan that is not a child of any parent).

In order to make the database resilient to crashes, it is common for B-Tree implementations to include an additional data structure on disk: write-ahead log AKA redo-log. This is an append-only file to which every B-Tree modification must be written before it can be applied to the pages of the tree itself. When the database comes back up after a crash, this log is used to restore the B-Tree back to a consistent state.

The additional complication of updating pages in place is that careful concurrency control is required if multiple threads are going to access the B-Tree at the same time, otherwise a thread may see the tree in an inconsistent state. This is typically done by protecting the tree’s data structures with latches(lightweight locks). Log-structured approaches are simpler in this regard, because they do all the merging in the background without interfering with incoming queries and atomically swap old segments for new segments from time to time.

Optimizations

• Instead of overwriting pages and maintaining a WAL for crash recovery, some databases use copy-on-write scheme. A modified page is written to a different location, and a new version of the parent page in the tree is created, pointing to the new location. This approach is also useful for concurrency control.
• We can save space in pages by not storing the entire key, but abbreviating it, especially in pages on the interior of the tree, keys only need to provide enough information to act as boundaries between key ranges. Packing more keys into a page allows the tree to have a higher branching factor, and thus fewer levels.
• Pages can be positioned anywhere on the disk, there is nothing requiring pages with nearby key ranges to be nearby on disk. If a query needs to scan over a large part of the key range in sorted order, that page-by-page layout can be inefficient, because a disk seek may be required for every page that is read. Therefore an optimization would be to lay out the tree so that leaf pages appear in sequential order in disk. However this has the complexity of maintaining order as the tree grows in size.
• We can introduce additional pointers to the nodes of the tree. For example, each leaf page may have references to its sibling pages to the left and right, which will allow scanning keys in order without jumping back to parent pages.