Hash tables and hash functions
We use hash maps/dictionaries in our day to day programming jobs, they are kind of a very fundamental data structure which when used correctly helps us reduce time-complexity of our operations. Ever wondered what are the fundamental concepts using which these beautiful data-structures are implemented? Well, that’s the topic of discussion in this page.
A hash-table is a data-structure which stores a mapping between a key to a value, this mapping has a worst case complexity of O(1) for the lookup/get(key) operation. Now these hash-tables are implemented differently in different languages(for example, in c++ map data structure uses a binary-search-tree, In java maps are implemented using arrays+linkedLists). I’ll not be going into the implementation details here.
Hash Functions
A function which maps a value from a large unbounded domain(pre-image) to a fixed smaller sized domain(image). As shown in the below diagram
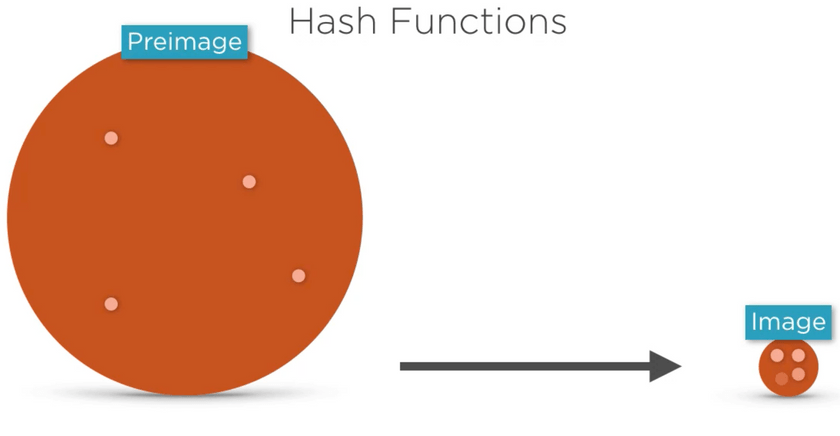
Hash-functions implementations(high level view)
-
A trivial thought process can be to map the key(in case of numbers) to themselves in the map, For example hash(1) = 1. Even though this implementation is
- fast(since no additional operation is required)
- perfect(since no two values map to the same key)
it isn’t random. i.e, it does not distribute the values evenly. We can easily predict what the mapping can be.
- Merkle-damgard construction which is usually used to hash a very large value. It usually divides the input into
fixed size chunks, a initial seed value and then iterates through these chunks by combining the current
chunk and the seed. This seed gets sent to the next chunk from the previous operation. The following diagrams depict
this concept

merkle-damgard-1 
merkle-damgard-2 
merkle-damgard-3 
merkle-damgard-4
K-independent hash-functions
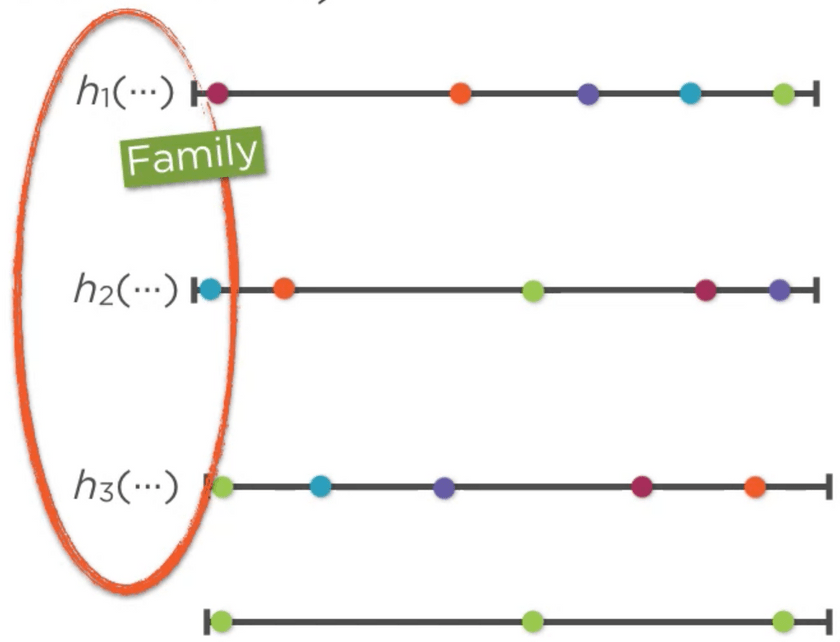
Instead of considering a single hash function, we can have a set of hash-functions, which can be used to distribute the hash-values randomly to a value domain. This set of hash-functions are called a family. Let’s consider a family with three hash functions h1, h2, h3, In order for this family to be considered 3-independent(since k=3), the following properties has to be satisfied
- Distribute the values evenly in the value domain for a given key. As show in the below diagram we can see
that the green value is distributed fairly uniformly in the value domain
even distribution - For any hash function in the family, either h1/h2/h3, if we pick any k keys, the values which is
produced should also be independent. For example, in our family if we consider h2, or any function for that
matter, the values which are mapped are independent indeed.
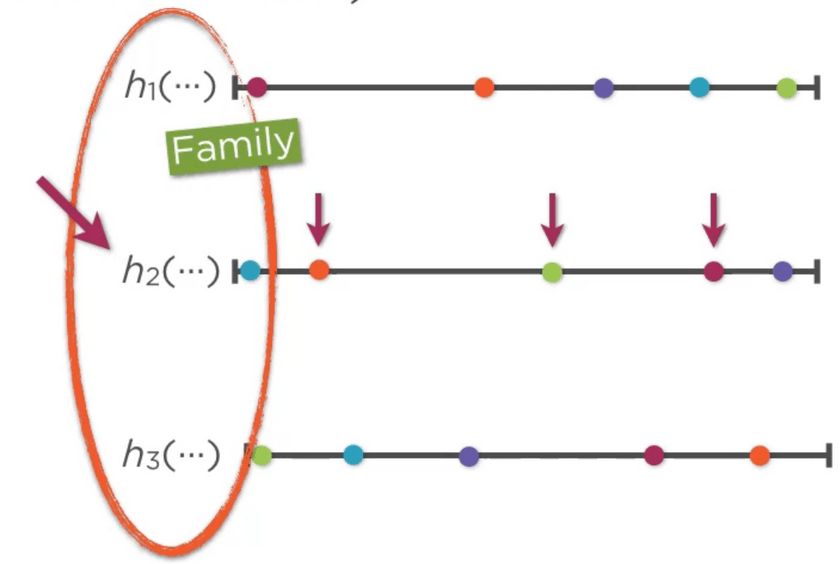
independent
When both of the above conditions are satisfied, we say that the family is k-independent.
Hash table with chaining
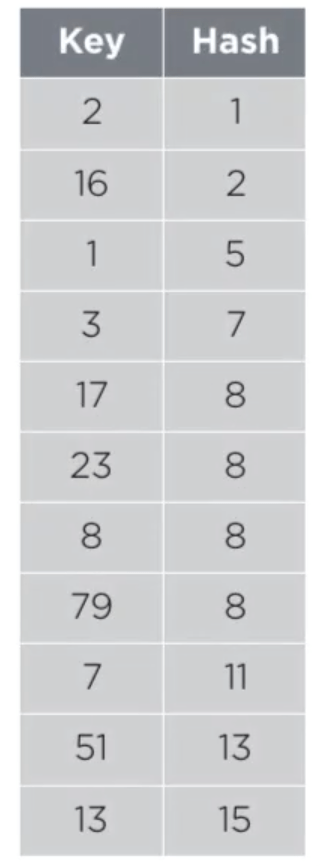
A common and a straight forward way to handle collisions in hash-tables is to use a linkedList to store all the values which map to a same key. For example, let’s say we have a hash function say hash(key) which results in the following outputs
- hash(17) = 8
- hash(23) = 8
- hash(8) = 8
- hash(79) = 8
- hash(2) = 1
- hash(16) = 3
- hash(1) = 5
- hash(3) = 7
- hash(19) = 9
- hash(7) = 11
- hash(0) = 13
- hash(13) = 15
the visual representation of the above operation can be represented as
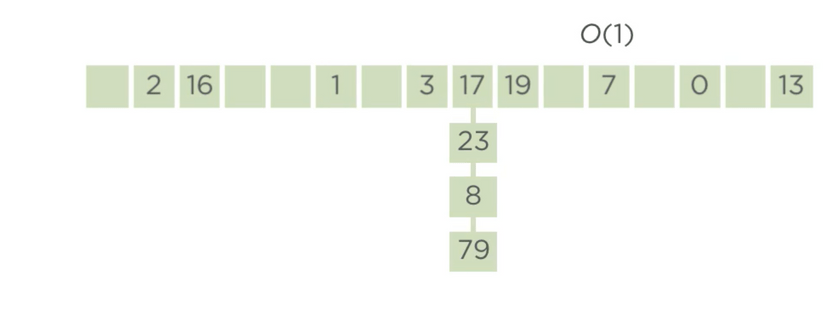
The above approach will result in a worst-case complexity of O(n) if all of the keys map to the same value in the table, since to find a value we need to scan all elements of the linkedList. Hence when constructing a hash table, the hash function used should result in minimum set of collisions.
Hash table with linear probing
Insertion
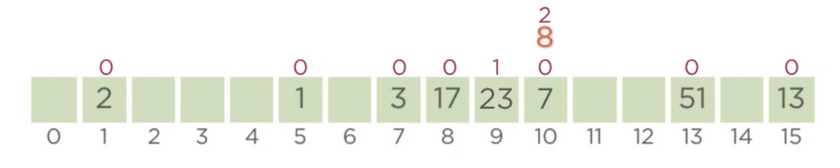
Using this technique, rather than inserting all the keys which map to the same hash in a linkedList we try to find alternative empty cells to insert them. For example, consider the key,hash combination as described in the below diagram
- 17 gets indexed to the index 8

17 - 23, maps to the value 8 but since index 8 is already occupied by 17, we choose the next available
index which is 9

23 - 8, also maps to the value 8, using the above algorithm we scan forward to find index 9 also occupied,
scanning again to one position to the right we find that index 10 is free, so 8 gets indexed at 10.

8 - 79, according to the same algorithm, we move forward to find the index 12 to be free and then 79 gets
indexed at position 12.

79
Lookup
Assuming the above example, the algorithm which is used is to scan forward until an empty index is found. The reasoning is that if we find an empty index either it should have been filled with the hash of the input key. If we are searching for 79 we start with the hash value 8 since that index isn’t occupied with the input key we scan forward until index 12.
Deletion
We do a search for the key in the mapped domain(image). Once the index is found, if we have more elements which are hashed to the same value we have to left-shift all of them. Otherwise the search will fail because we’ll have an empty index. We do this scan for all the keys which map to the same hash on the right of the key to be deleted.
Complexity
- Insertion - O(N) worst case
- Lookup - O(N) worst case
- Deletion - O(N) worst case
Robin Hood Hashing(variant of linear probing)
Assuming the same input example which is shown above

The keys which are indexed without collision are as shown below

With robin hood hashing we have the concept of a probe-position, which is the distance of the current index from the original index/position specified by its hash-value. If we assume that this be denoted by pp, then pp(17) is 0, since 17 hashes to 8 and it is placed at the same index.
The algorithm says, we’ll have to switch the key to be inserted(key-insert) with the current key(key-current), if pp(key-insert) > pp(key-current). We could say that a key which takes a shorter time to search for is rich, with a shorter pp, and similarly a key which takes a greater time to search for is poor with a greater pp. Hence, intuitively we can see that the algorithm steals the index from rich keys and gives it to the poor keys, that’s the reason behind the name for this algorithm.
Insertion
- 23, we see that bucket/index 8 is occupied, we can also see that there is an empty index immediately to the
right, hence 23 gets indexed over there with a pp of 1.

23 - 8, also has the hash value of 8, we try the next index by incrementing our current probe position pp(8)++
which results in 1, to see that the next index is also occupied by 23 and pp(23)=1. Hence, both 23 and
8 are equal in terms of wealth, we move forward by incrementing the probe position of 8 further(pp(8)=2).
The index which is found now, has been occupied with 7 with a pp=0, according to our algorithm, there’s a
difference in wealth here, hence 8 gets indexed at 10, and 7 is moved out. Subsequently if we increment the
probe position of 7 we find that the index 11 is empty and thus 7 gets indexed at 11 with a pp=1.
8 
8 
8
We can notice that using this approach, we maintain elements in order of increasing probe positions, and also keys with same hash values are kept together. This clearly is a performance advantage w.r.t memory access. We can say that the expected time complexity is O(1) provided the hash-function used is sufficiently random. But the worst-case complexity is still O(N).
Lookup
As with regular linear probing the algorithm is to scan forward for the elements if the hash value isn’t same as the key which is being searched for. This results in the best case complexity of O(1), but the worst case is still O(N).
Deletion
There are multiple approaches for deletion, but a commonly used approach is space shifting. Which goes like this, find an empty bucket or a bucket with probe position=0 and shift all of these elements until this index, to the left and decrease each of their probe position by 1.
For example, let’s say 8 has to be deleted, first step is to search for 8 which results in index 10. Index 10 gets emptied, and we search for an empty index or an index with an element with probe position 0. This results in 51, hence the elements 79, 1 get shifted to the left and their probe positions are decreased by 1.

Conclusion This was a very high level view of how the various hash-functions are implemented in practice. The actual implementations involve a high degree of mathematics. Some references are given below

